Bihar Board 12th Maths Objective Answers Chapter 10 Vector Algebra

Bihar Board 12th Maths Objective Questions and Answers

Bihar Board 12th Maths Objective Answers Chapter 10 Vector Algebra

Question 1.
If \(\left(\frac{1}{2}, \frac{1}{3}, n\right)\) are the direction cosines of a line, then the value of n is
(a) \(\frac{\sqrt{23}}{6}\)
(b) \(\frac{23}{6}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{3}{2}\)
Answer:
(a) \(\frac{\sqrt{23}}{6}\)

Question 2.
Find the magnitude of vector \(3 \hat{i}+2 \hat{j}+12 \hat{k}\).
(a) √157
(b) 4√11
(c) √213
(d) 9√3
Answer:
(a) √157

Direction (3 – 5): Study the given parallelogram and answer the following questions.

Question 3.
Which of the following represents equal vectors?
(a) a, c
(b) b, d
(c) b, c
(d) m, d
Answer:
(b) b, d

Question 4.
Which of the following represents collinear but not equal vectors?
(a) a, c
(b) b, d
(c) b, m
(d) Both (a) and (b)
Answer:
(a) a, c

Question 5.
Which of the following represents coinitial vector?
(a) c, d
(b) m, b
(c) b, d
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 6.
The unit vector in the direction of the sum of vectors

Answer:
(a) \(\frac{1}{5 \sqrt{2}}(3 \hat{i}+4 \hat{j}+5 \hat{k})\)

Question 7.
The vectors \(3 \hat{i}+5 \hat{j}+2 \hat{k}, 2 \hat{i}-3 \hat{j}-5 \hat{k}\) and \(5 \hat{i}+2 \hat{j}-3 \hat{k}\) form the sides of
(a) Isosceles triangle
(b) Right triangle
(c) Scalene triangle
(d) Equilaterala triangle
Answer:
(d) Equilaterala triangle

Question 8.

Answer:
(d) α = ±1, β = 1

Question 9.
The vectors \(a=x \hat{i}-2 \hat{j}+5 \hat{k}\) and \(b=\hat{i}+y \hat{j}-z \hat{k}\) are collinear, if
(a) x =1, y = -2, z = -5
(b) x= 1.2, y = -4, z = -10
(c) x = -1/2, y = 4, z = 10
(d) All of these
Answer:
(d) All of these

Question 10.
The vector \(\hat{i}+x \hat{j}+3 \hat{k}\) is rotated through an angle θ and doubled in magnitude, then it becomes \(4 \hat{i}+(4 x-2) \hat{i}+2 \hat{k}\). The value of x is
(a) \(\left\{-\frac{2}{3}, 2\right\}\)
(b) \(\left\{\frac{1}{3}, 2\right\}\)
(c) \(\left\{\frac{2}{3}, 0\right\}\)
(d) {2, 7}
Answer:
(a) \(\left\{-\frac{2}{3}, 2\right\}\)

Question 11.
Three points (2, -1, 3), (3, -5, 1)and (-1, 11, 9) are
(a) Non-collinear
(b) Non-coplanar
(c) Collinear
(d) None of these
Answer:
(c) Collinear

Question 12.
The points with position vectors \(60 \hat{i}+3 \hat{j}, 40 \hat{i}-8 \hat{j}\) and \(a \hat{i}-5 \hat{j}\) are collinear if
(a) a = -40
(b) a = 40
(c) a = 20
(d) None of these
Answer:
(a) a = -40

Question 13.
The position vectors of the points A, B, C are \((2 \hat{i}+\hat{j}-\hat{k}),(3 \hat{i}-2 \hat{j}+\hat{k})\) and \((\hat{i}+4 \hat{j}-3 \hat{k})\) respectively. These points
(a) form an isosceles triangle
(b) form a right angled triangle
(c) are collinear
(d) form a scalene triangle
Answer:
(a) form an isosceles triangle

Question 14.
The figure formed by the four points \(\hat{i}+\hat{j}-\hat{k}\), \(2 \hat{i}+3 \hat{j}, 5 \hat{j}-2 \hat{k}\) and \(\hat{k}-\hat{j}\) is
(a) trapezium
(b) rectangle
(c) parallelogram
(d) None of these
Answer:
(d) None of these

Question 15.
If x coordinate of a point P of a line joining the points Q(2, 2, 1) and R(5, 2, -2) is 4, then the z coordinate of P is
(a) -2
(b) -1
(c) 1
(d) 2
Answer:
(b) -1

Question 16.
If O is origin and C is the mid point of A(2, -1) and B(-4, 3), then the value of OC is
(a) \(\hat{i}+\hat{j}\)
(b) \(\hat{i}-\hat{j}\)
(c) \(-\hat{i}+\hat{j}\)
(d) \(-\hat{i}-\hat{j}\)
Answer:
(c) \(-\hat{i}+\hat{j}\)

Question 17.
The vectors AB = \(3 \hat{i}+4 \hat{k}\) and AC = \(A C=5 \hat{i}-2 \hat{j}+4 \hat{k}\) are the side of a ΔABC. The length of the median through A is
(a) √18
(b) √72
(c) √33
(d) √288
Answer:
(c) √33

Question 18.
The summation of two unit vectors is a third unit vector, then the modulus of the difference of the unit vector is
(a) √3
(b) 1 – √3
(c) 1 + √3
(d) -√3
Answer:
(a) √3

Question 19.

Answer:
(d) \(\frac{1}{\sqrt{6}}(2 \hat{i}-\hat{j}+\hat{k})\)

Question 20.

Answer:
(c) \(\pi \geq \theta>\frac{2 \pi}{3}\)

Question 21.
Let a, b and c be vectors with magnitudes 3, 4 and 5 respectively and a + b + c = 0, then the values of a.b + b.c + c.a is
(a) 47
(b) 25
(c) 50
(d) -25
Answer:
(d) -25

Question 22.
If |a| = |b| = 1 and |a + b| = √3, then the value of (3a – 4b).(2a + 5b) is
(a) -21
(b) \(-\frac{21}{2}\)
(c) 21
(d) \(\frac{21}{2}\)
Answer:
(b) \(-\frac{21}{2}\)

Question 23.

Answer:
(c) \(\frac{1}{\sqrt{2}}(\hat{i}+\hat{j})\)

Question 24.
If |a – b| = |a| = |b| = 1, then the angle between a and b is
(a) \(\frac{\pi}{3}\)
(b) \(\frac{3 \pi}{4}\)
(c) \(\frac{\pi}{2}\)
(d) 0
Answer:
(a) \(\frac{\pi}{3}\)

Question 25.

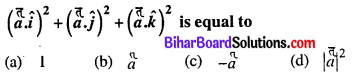
Answer:
(d) |a|²

Question 26.
a, b, c are three vectors, such that a + b + c = 0, |a|= 1, |b|= 2, |c|= 3, then a.b + b.c + c is equal to
(a) 0
(b) -7
(c) 7
(d) 1
Answer:
(b) -7

Question 27.
If |a + b| = |a – b|, then angle between a and b is (a ≠ 0, b ≠ 0)
(a) \(\frac{\pi}{3}\)
(b) \(\frac{\pi}{6}\)
(c) \(\frac{\pi}{4}\)
(d) \(\frac{\pi}{2}\)
Answer:
(d) \(\frac{\pi}{2}\)

Question 28.
If a and b are two unit vectors inclined to x-axis at angles 30° and 120° respectively, then |a + b| equals
(a) \(\sqrt{\frac{2}{3}}\)
(b) √2
(c) √3
(d) 2
Answer:
(d) 2

Question 29.
If the angle between \(\hat{i}+\hat{k}\) and \(\hat{i}+\hat{j}+a \hat{k}\) is \(\frac{\pi}{3}\), then the value of a is
(a) 0 or 2
(b) -4 or 0
(c) 0 or -3
(d) 2 or -2
Answer:
(b) -4 or 0

Question 30.
The length of longer diagronai of the parallelogram constructed on 5a + 2b and a – 3b. If it is given that
|a| = 2√2, |b| = 3 and angle between a and b is \(\frac{\pi}{4}\), is
(a) 15
(b) √113
(c) √593
(d) √369
Answer:
(c) √593

Question 31.
If a, b, c are unit vectors, then |a – b| + |b – c| + |c – a| does not exceed
(a) 4
(b) 9
(c) 8
(d) 6
Answer:
(b) 9

Question 32.
Find the value of λ so that the vectors \(2 \hat{i}-4 \hat{j}+\hat{k}\) and \(4 \hat{i}-8 \hat{j}+\lambda \hat{k}\) are perpendicular.
(a) -15
(b) 10
(c) -40
(d) 20
Answer:
(c) -40

Question 33.
The dot product of a vector with the vectors \(\hat{i}+\hat{j}-3 \hat{k}, \hat{i}+3 \hat{j}-2 \hat{k}\) and \(2 \hat{i}+\hat{j}+4 \hat{k}\) are 0, 5 and 8 respectively. Find the vector.
(a) \(\hat{i}+2 \hat{j}+\hat{k}\)
(b) \(-\hat{i}+3 \hat{j}-2 \hat{k}\)
(c) \(\hat{i}+2 \hat{j}+3 \hat{k}\)
(d) \(\hat{i}-3 \hat{j}-3 \hat{k}\)
Answer:
(a) \(\hat{i}+2 \hat{j}+\hat{k}\)

Question 34.
If a, b, c are three mutually perpendicular vectors of equal magnitude, find the angle between a and a + b + c.
(a) \(\cos ^{-1}(1 / \sqrt{3})\)
(b) \(\cos ^{-1}(1 / 2 \sqrt{2})\)
(c) \(\cos ^{-1}(1 / 3 \sqrt{3})\)
(d) \(\cos ^{-1}(1 / 2 \sqrt{3})\)
Answer:
(a) \(\cos ^{-1}(1 / \sqrt{3})\)

Question 35.
Find the angle between the vectors a + b and a – b if a = \(2 \hat{i}-\hat{j}+3 \hat{k}\) and b = \(b=3 \hat{i}+\hat{j}-2 \hat{k}\)
(a) \(\frac { \pi }{ 6 }\)
(b) \(\frac { \pi }{ 3 }\)
(c) \(\frac { \pi }{ 2 }\)
(d) 0
Answer:
(c) \(\frac { \pi }{ 2 }\)

Question 36.
If a = \(2 \hat{i}+\hat{j}+2 \hat{k}\) and b = \(5 \hat{i}-3 \hat{j}+\hat{k}\), then the projection of b on a is
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(a) 3

Question 37.
Let \(a=\hat{i}+2 \hat{j}+\hat{k}, b=\hat{i}-\hat{j}+\hat{k}, c=\hat{i}+\hat{j}-\hat{k}\). A vector coplanar to a and b has a projection along c of magnitude \(\frac{1}{\sqrt{3}}\), then the vector is
(a) \(4 \hat{i}-\hat{j}+4 \hat{k}\)
(b) \(4 \hat{i}+\hat{j}-4 \hat{k}\)
(c) \(2 \hat{i}+\hat{j}+\hat{k}\)
(d) None of these
Answer:
(a) \(4 \hat{i}-\hat{j}+4 \hat{k}\)

Question 38.
The component of i in the direction of the vector \(\hat{i}+\hat{j}+2 \hat{k}\) is
(a) √6
(b) 6
(c) 6√6
(d) \(\frac{\sqrt{6}}{6}\)
Answer:
(d) \(\frac{\sqrt{6}}{6}\)

Question 39.
Find the projection of b + c on a where a = \(\hat{i}+2 \hat{j}+\hat{k}\), b = \(\hat{i}+3 \hat{j}+\hat{k}\) and c = \(\hat{i}+\hat{k}\).
(a) \(\frac { 5 }{ \surd 3 }\)
(b) 2√2
(c) \(\frac { 3 }{ \surd 2 }\)
(d) \(\frac { 10 }{ \surd 6 }\)
Answer:
(d) \(\frac { 10 }{ \surd 6 }\)

Question 40.
If a = \(\hat{i}+\hat{j}+\hat{k}\), b = \(\hat{i}+3 \hat{j}+5 \hat{k}\) and c = \(7 \hat{i}+9 \hat{j}+11 \hat{k}\), then the area of parallelogram having diagonals a + b and b + c is
(a) 4√6
(b) \(\frac{1}{2} \sqrt{21}\)
(c) \(\frac{\sqrt{6}}{2}\)
(d) √6
Answer:
(a) 4√6

Question 41.

Answer:
(c) \(\frac{3 \hat{i}-2 \hat{j}+6 \hat{k}}{7}\)

Question 42.
The area of parallelogram whose adjacent sides are \(\hat{i}-2 \hat{j}+3 \hat{k}\) and \(2 \hat{i}+\hat{j}-4 \hat{k}\) is
(a) 10√6
(b) 5√6
(c) 10√3
(d) 5√3
Answer:
(b) 5√6

Question 43.
If AB × AC = \(2 \hat{i}-4 \hat{j}+4 \hat{k}\), then the are of ΔABC is
(a) 3 sq. units
(b) 4 sq. units
(c) 16 sq. units
(d) 9 sq. units
Answer:
(a) 3 sq. units

Question 44.

Answer:
(a) \(\frac{5 \sqrt{3}}{3}(\hat{i}+\hat{j}+\hat{k})\)

Question 45.
|a × b|² + |a.b|² = 144 and |a| = 4, then |b| is equal to
(a) 12
(b) 3
(c) 8
(d) 4
Answer:
(b) 3

Question 46.
If |a × b| = 4 and |a.b| = 2, then |a|² |b|² is equal to
(a) 2
(b) 6
(c) 8
(d) 20
Answer:
(d) 20

Question 47.

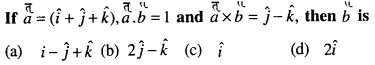
Answer:
(c) \(\hat{i}\)

Question 48.
The two vectors a = \(2 \hat{i}+\hat{j}+3 \hat{k}\) and b = 4 \hat{i}-\lambda \hat{j}+6 \hat{k} ae parallel, if λ is equal to
(a) 2
(b) -3
(c) 3
(d) 2
Answer:
(d) 2

Question 49.
If |a|= 5, |b|= 13 and |a × b|= 25, find a.b
(a) ±10
(b) ±40
(c) ±60
(d) ±25
Answer:
(c) ±60

Question 50.
Find the value of λ so that the vectors \(2 i-4 \hat{j}+\hat{k}\) and \(4 i-8 \hat{j}+\lambda \hat{k}\) are parallel.
(a) -1
(b) 3
(c) -4
(d) 2
Answer:
(d) 2

Question 51.
If a + b + c = 0, then a × b =
(a) c × a
(b) b × c
(c) 0
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 52.
If a is perpendicular to b and c, |a| = 2, |b| = 3, |c| = 4 and the angle between b and c is \(\frac{2 \pi}{3}\), |abc| is equal to
(a) 4√3
(b) 6√3
(c) 12√3
(d) 18√3
Answer:
(c) 12√3

Question 53.

Answer:
(b) a

Question 54.

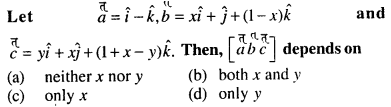
Answer:
(a) neither x nor y

Question 55.
If a, b, c are three non-coplanar vectors, then (a + b + c).[(a + b) × (a + c)] is
(a) 0
(b) 2[abc]
(c) -[abc]
(d) [abc]
Answer:
(c) -[abc]

Question 56.
If u, v and w are three non-coplanar vectors, then (u + v – w).[(u – v) × (v – w)] equals
(a) 0
(b) u.v × w
(c) u.w × v
(d) 3u.v × w
Answer:
(b) u.v × w

Question 57.
If unit vector c makes an angle \(\frac{\pi}{3}\) with \(\hat{i} \times \hat{j}\), then minimum and maximum values of \((\hat{i} \times \hat{j}) \cdot c\) respectively are
(a) 0, \(\frac{\sqrt{3}}{2}\)
(b) \(-\frac{\sqrt{3}}{2}, \frac{\sqrt{3}}{2}\)
(c) -1, \(\frac{\sqrt{3}}{2}\)
(d) None of these
Answer:
(b) \(-\frac{\sqrt{3}}{2}, \frac{\sqrt{3}}{2}\)

Question 58.
The volume of the tetrahedron whose conterminous edges are \(\hat{j}+\hat{k}, \hat{i}+\hat{k}, i+\hat{j}\) is
(a) \(\frac{1}{6}\) cu. unit
(b) \(\frac{1}{3}\) cu. unit
(c) \(\frac{1}{2}\) cu. unit
(d) \(\frac{2}{3}\) cu. unit
Answer:
(b) \(\frac{1}{3}\) cu. unit

Question 59.
If the vectors \(2 \hat{i}-3 \hat{j}, i+\hat{j}-\hat{k}\) and \(3 \hat{i}-\hat{k}\) form three concurrent edges of a parallelopiped, then the volume of the parallelopiped is
(a) 8
(b) 10
(c) 4
(d) 14
Answer:
(c) 4

Question 60.
The volume of the parallelopiped whose edges are represented by \(-12 \hat{i}+\alpha \hat{k}, 3 j-\hat{k}\) and \(2 \hat{i}+j-15 \hat{k}\) is 546 cu. units. Then α =
(a) 3
(b) 2
(c) -3
(d) -2
Answer:
(c) -3

Question 61.

Answer:
(d) None of these

Question 62.

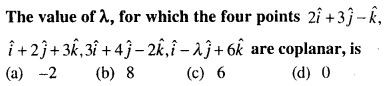
Answer:
(a) -2

Question 63.

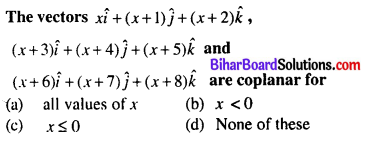
Answer:
(a) all values of x

Question 64.
If the vectors \(\hat{i}-2 \hat{j}+3 \hat{k},-2 \hat{i}+3 \hat{j}-4 \hat{k}, \lambda \hat{i}-\hat{j}+2 \hat{k}\) are coplanar, then the value of λ is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(a) 0

Question 65.
Find the value of λ if the vectors, a = \(2 \hat{i}-\hat{j}+\hat{k}\), b = \(\hat{i}+2 \hat{j}-3 \hat{k}\) and c = \(3 \hat{i}-\lambda \hat{j}+5 \hat{k}\) are coplanar.
(a) 4
(b) -2
(c) -6
(d) 5
Answer:
(a) 4

Question 66.
Find λ if the vectors \(\hat{i}-\hat{j}+\hat{k}, 3 \hat{i}+\hat{j}+2 \hat{k}\) and \(\hat{i}+\lambda \hat{j}-\hat{k}\) are coplanar.
(a) 5
(b) 12
(c) 15
(d) 8
Answer:
(c) 15

Question 67.
The vector in the direction of the vector \(\hat{i}-2 \hat{j}+2 \hat{k}\) that has magnitude 9 is

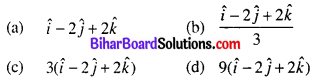
Answer:
(c) \(3(\hat{i}-2 \hat{j}+2 \hat{k})\)

Question 68.
The position vector of the point which divides the join of points 2a – 3b and a + b in the ratio 3 : 1 is

Answer:
(d) \(\frac{5 a}{4}\)

Question 69.
The angle between two vectors a and b with magnitudes √3 and 4, respectively and a.b = 2√3 is
(a) \(\frac{\pi}{6}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{2}\)
(d) \(\frac{5 \pi}{2}\)
Answer:
(b) \(\frac{\pi}{3}\)

Question 70.
Find the value of λ such that the vectors a = \(2 \hat{i}+\lambda \hat{j}+\hat{k}\) and b = \(\hat{i}+2 \hat{j}+3 \hat{k}\) are orthogonal.
(a) 0
(b) 1
(c) \(\frac{3}{2}\)
(d) \(-\frac{5}{2}\)
Answer:
(d) \(-\frac{5}{2}\)

Question 71.
The value of λ for which the vectors \(3 \hat{i}-6 \hat{j}+\hat{k}\) and \(2 \hat{i}-4 \hat{j}+\lambda \hat{k}\) are parallel is
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{5}{2}\)
(d) \(\frac{2}{5}\)
Answer:
(a) \(\frac{2}{3}\)

Question 72.
The vectors from origin to the points A and B are a = \(2 \hat{i}-3 \hat{j}+2 \hat{k}\) and b = \(2 \hat{i}+3 \hat{j}+\hat{k}\), respectively then the area of triangle OAB is
(a) 340
(b) √25
(c) √229
(d) \(\frac{1}{2}\) √229
Answer:
(d) \(\frac{1}{2}\) √229

Question 73.
The vectors \(\lambda \hat{i}+\hat{j}+2 \hat{k}, \hat{i}+\lambda \hat{j}-\hat{k}\) and \(2 \hat{i}-\hat{j}+\lambda \hat{k}\) are coplanar if
(a) λ = -2
(b) λ = 0
(c) λ = 1
(d) λ = -1
Answer:
(a) λ = -2

Question 74.
If a, b, c are unit vectors such that a + b + c = 0, then the value of a.b + b.c + c.a is
(a) 1
(b) 3
(c) \(-\frac{3}{2}\)
(d) None of these
Answer:
(c) \(-\frac{3}{2}\)

Question 75.
If |a| = 4 and -3 ≤ λ ≤ 2, then the range of |λa| is
(a) [0, 8]
(b) [-12, 8]
(c) [0, 12]
(d) [8, 12]
Answer:
(c) [0, 12]

Question 76.
The number of vectors of unit length perpendicular to the vectors a = \(2 \hat{i}+\hat{j}+2 \hat{k}\) and b = \(\hat{j}+\hat{k}\) is
(a) one
(b) two
(c) three
(d) infinite
Answer:
(b) two