Bihar Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.4 Text Book Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.4
Bihar Board Class 10 Maths द्विघात समीकरण Ex 4.4
प्रश्न 1.
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का अस्तित्व हो, तो उन्हें ज्ञात कीजिए :
(i) 2x2 – 3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
हल
(i) दिया गया समीकरण :
2x2 – 3x + 5 = 0
उपर्युक्त समीकरण, की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = 2, b = -3 तथा c = 5
विविक्तकर, D = b2 – 4ac
=(-3)2 – 4 × 2 × 5
= 9 – 40
= -31 (ऋणात्मक)
∵ विविक्तकर D ऋणात्मक है।
∵ समीकरण के मूल काल्पनिक हैं।
अतः समीकरण के मूल अधिकल्पित हैं या मूलों का अस्तित्व नहीं है।
(ii) दिया गया समीकरण :
3x2 – 4√3x + 4 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = 3, b = -4√3 तथा c = 4
विविक्तकर, D = b2 – 4ac
=(-4√3)2 – 4 × 3 × 4
= 48 – 48
= शून्य
विविक्तकर D = 0; अत: समीकरण के मूल वास्तविक और समान हैं।

मूल दो हैं जो परस्पर समान हैं;
अत: समीकरण के मूल = \(\frac{2}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
(iii) दिया गया समीकरण :
2x2 – 6x + 3 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = 2, b = -6 तथा c = 3
विविक्तकर, D = b2 – 4ac
= (-6)2 – 4 × 2 × 3
= 36 – 24
= 12
विविक्तकर, D > 0; अत: समीकरण के मूल वास्तविक और असमान हैं।

![]()
प्रश्न 2.
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों।
(i) 2x2 + kx + 3 = 0
(ii) kx(x – 2) + 6 = 0
हल
(i) दिया गया समीकरण : 2x2 + kx + 3 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = 2, b = k तथा c = 3
विविक्तकर, D = b2 – 4ac
= k2 – 4 × 2 × 3
= k2 – 24
समीकरण के मूल समान हैं। तब, विविक्तकर, D = 0
k2 – 24 = 0
⇒ k2 = 24
⇒ k = ±√24 = ±2√6
अत: मूल बराबर होने के लिए k = ±2√6 होना चाहिए।
(ii) दिया गया समीकरण :
kx(x – 2) + 6 = 0
⇒ kx2 – 2kx + 6 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = k, b = -2k तथा c = 6
विविक्तकर, D = b2 – 4ac
= (-2k)2 – 4 × k × 6
= 4k2 – 24k
= 4k(k – 6)
समीकरण के मूल बराबर हैं, तब विविक्तकर, D = 0
4k(k – 6) = 0
यदि 4k = 0 तो k = 0
और यदि (k – 6) = 0 तो k = 6
अत: समीकरण के मूल बराबर होने के लिए k = 6 होना चाहिए क्योंकि k = 0 प्रतिबन्धित होता है।
![]()
प्रश्न 3.
क्या एक ऐसी आम की बगिया बनाना सम्भव है जिसकी लम्बाई, चौड़ाई से दुगुनी हो और उसका क्षेत्रफल 800 m2 हो? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल
माना आम की बगिया की चौड़ाई x m है।
लम्बाई, चौड़ाई की दुगुनी है।
लम्बाई = 2x m
बगिया का क्षेत्रफल = लम्बाई × चौड़ाई = 2x × x = 2x2 m2
परन्तु, दिया है कि बगिया का क्षेत्रफल = 800 m2
2x2 = 800
⇒ x2 = 400
⇒ x = ±√400 = ± 20 m
तब, बगिया की चौड़ाई = 20 m (∵ चौड़ाई ऋणात्मक नहीं हो सकती)
बगिया की लम्बाई = 2x = 2 × 20 = 40 m
अत: आम की बगिया सम्भव है और उसकी लम्बाई 40 m व चौड़ाई 20 m होगी।
प्रश्न 4.
क्या निम्न स्थिति सम्भव है? यदि है, तो उनकी वर्तमान आयु ज्ञात कीजिए :
दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयु (वर्षों में) का गुणनफल 48 था।
हल
माना एक मित्र की आयु x वर्ष है।
दोनों का आयु का योग 20 वर्ष है।
दूसरे मित्र की आयु = (20 – x) वर्ष
4 वर्ष पूर्व पहले मित्र की आयु = (x – 4) वर्ष
तथा 4 वर्ष पूर्व दूसरे मित्र की आयु = (20 – x – 4) = (16 – x) वर्ष
तब, 4 वर्ष पूर्व दोनों की आयु का गुणनफल = (x – 4) (16 – x)
= 16x – x2 – 64 + 4x
= -x2 + 20x – 64
दिया है, गुणनफल = 48
48 = -x2 + 20x – 64
⇒ x2 – 20x + 64 + 48 = 0
⇒ x2 – 20x + 112 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = 1, b = -20 तथा c = 112
तब, विविक्तकर, D = b2 – 4ac
= (-20)2 – 4 × 1 × 112
= 400 – 448
= -48
विविक्तकर D ऋणात्मक है।
समीकरण के मूल अधिकल्पित हैं।
अत: ऐसी स्थिति सम्भव नहीं है।
![]()
प्रश्न 5.
क्या परिमाप 80 m तथा क्षेत्रफल 400 m2 के एक पार्क को बनाना सम्भव है? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल
माना पार्क की लम्बाई x m है।
दिया है, पार्क का परिमाप = 80 m
⇒ 2 (लम्बाई + चौड़ाई) = 80 m
⇒ 2(x + चौड़ाई) = 80
⇒ x + चौड़ाई = 40
⇒ चौड़ाई = (40 – x) m
तब, पार्क का क्षेत्रफल = लम्बाई × चौड़ाई
= x(40 – x)
= (40x – x2) m2
परन्तु प्रश्नानुसार पार्क का क्षेत्रफल 400 m2 है।
400 = 40x – x2
⇒ x2 – 40x + 400 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax2 + bx + c = 0 से करने पर,
a = 1, b = -40 तथा c = 400
विविक्तकर, D = b2 – 4ac
= (-40)2 – 4 × 1 × 400
= 1600 – 1600
= 0
विविक्तकर, D = 0;
अत: समीकरण के मूल समान हैं।
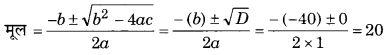
प्रत्येक मूल 20 है।
अत: ऐसा पार्क सम्भव है और उसकी लम्बाई व चौड़ाई में से प्रत्येक 20 m होगी।