Bihar Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.2

Bihar Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.2 Text Book Questions and Answers.

BSEB Bihar Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.2

Bihar Board Class 10 Maths त्रिकोणमिति का परिचय Ex 8.2

प्रश्न 1.
निम्नलिखित के मान निकालिए
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°

हल

प्रश्न 2.
सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए-
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}=\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°

(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=\)
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0

(iii) sin 2A = 2sin A तब सत्य होता है, जबकि A बराबर है :
(A) 0°
(B) 30°
(C) 45°
(D) 60°

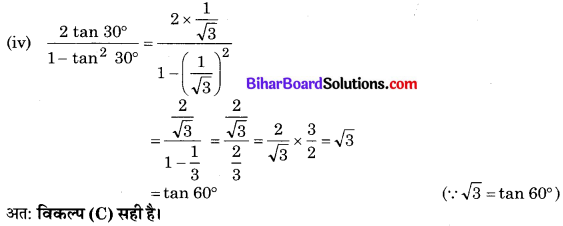
(iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) बराबर है :
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
हल

प्रश्न 3.
यदि tan(A + B) = √3 और tan(A – B) = \(\frac{1}{\sqrt{3}}\); 0° < A + B < 90°; A > B, तो A और B का मान ज्ञात कीजिए।
हल
दिया है, tan (A + B) = √3
⇒ tan (A + B) = tan 60°
⇒ A + B = 60° ……(1)
तथा tan (A – B) = \(\frac{1}{\sqrt{3}}\)
⇒ tan (A – B) = tan 30°
⇒ A – B = 30° …….(2)
समीकरण (1) व (2) को हल करने पर,
अत: A = 45° तथा B = 15°

प्रश्न 4.
बताइए कि निम्नलिखित में कौन-कौन सत्य हैं या असत्य हैं। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) sin(A + B) = sin A + sin B
(ii) θ में वृद्धि होने के साथ sin θ के मान में भी वृद्धि होती है।
(iii) θ में वृद्धि होने के साथ cos θ के मान में भी वृद्धि होती है।
(iv) θ के सभी मानों पर sin θ = cos θ
(v) A = 0° पर cot A परिभाषित नहीं है।
हल
(i) माना A = 30° तथा B = 30°, तब
sin (A + B) = sin (30° + 30° ) = sin 60° = \(\frac{\sqrt{3}}{2}\)
और sin A + sin B = sin 30° + sin 30° = \(\frac{1}{2}+\frac{1}{2}\) = 1
sin (A + B) ≠ sin A + sin B
अत: दिया गया कथन असत्य है।

(ii) ∵ sin 0° = 0, sin 30° = \(\frac{1}{2}\), sin 45° = \(\frac{1}{\sqrt{2}}\), sin 60° = \(\frac{\sqrt{3}}{2}\), sin 90° = 1
स्पष्ट है कि θ का मान बढ़ने पर sin θ का मान भी बढ़ता है परन्तु यह θ = 90° तक ही सही है, आगे नहीं।
अत: दिया गया कथन सत्य है।

(iii) ∵ cos 0° = 1 और cos 90° = 0
स्पष्ट है कि θ का मान बढ़ने पर cos θ में वृद्धि नहीं होती।
अत: दिया गया कथन असत्य है।

(iv) ∵ sin θ = cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1
⇒ tan θ = 1
⇒ θ = 45°
θ के सभी मानों के लिए sin θ ≠ cos θ
अतः दिया गया कथन असत्य है।

(v) त्रिकोणमितीय अनुपातों के विभिन्न मानों के लिए संकलित सारणी को देखने से स्पष्ट है कि cot A = अनिर्धारित
∴ A = 0° पर cot A परिभाषित नहीं (not defined) है।
अत: दिया गया कथन सत्य है।