Bihar Board Class 11 Physics Solutions Chapter 11 द्रव्य के तापीय गुण Textbook Questions and Answers, Additional Important Questions, Notes.
BSEB Bihar Board Class 11 Physics Solutions Chapter 11 द्रव्य के तापीय गुण
Bihar Board Class 11 Physics द्रव्य के तापीय गुण Text Book Questions and Answers
अभ्यास के प्रश्न एवं उनके उत्तर
प्रश्न 11.1
निऑन तथा CO2 के त्रिक बिन्दु क्रमश: 24.57 K तथा 216.55 K हैं। इन तापों को सेल्सियस तथा फारेनहाइट मापक्रमों में व्यक्त कीजिए।
उत्तर:
दिया है:
निऑन का त्रिक बिन्दु, T1 = 24.57 K CO2 का त्रिक बिन्दु, T2 = 216.55 K
हम जानते हैं कि केल्विन सेल्यिस व फारेनहाइट पैमाने में निम्नवत् सम्बन्ध है –
\(\frac{C-O}{100-O}\) = \(\frac{F-32}{212-32}\)
= \(\frac{T-273.15}{100}\)
सेल्सियस पैमाने पर,
\(\frac{C-O}{100-O}\) = \(\frac{T-273.15}{100}\)
या C – T = 273.15
Ne के लिए
t°1 C = 24.57 – 273.15
= -248.58°C CO2 के लिए
t°2 C = 216.55 – 273.15 = -55.6°C
फारेनहाइट पैमाने पर,
\(\frac{F-32}{180}\) = \(\frac{T-273.14}{100}\)
Ne के लिए,
F1 = (T1 – 273.15) × \(\frac{9}{5}\) + 32
= (24.57 – 273.15) × \(\frac{9}{5}\) + 32
= -248.58 × \(\frac{9}{5}\) + 32
= -415.26°F
CO2 के लिए,
F2 = (T2 – 273.15) × \(\frac{9}{5}\) + 32
= (216.55 – 273.15) \(\frac{9}{5}\) + 32
= -56.6 × \(\frac{9}{5}\) + 32 = -69.88°F
![]()
प्रश्न 11.2
दो परम ताप मापक्रमों A तथा B पर जल के त्रिक बिन्दु को 200 A तथा 350 B द्वारा परिभाषित किया गया है। TA तथा TB में क्या सम्बन्ध है?
उत्तर:
माना दोनों का शून्य, परम शून्य ताप से सम्पाती है। प्रश्नानुसार, प्रथम पैमाने पर परम शून्य से जल के त्रिक बिन्दु तक के तापों को 200 भागों में एवम् दूसरे पैमाने पर 350 भागों में विभाजित किया गया है।
∴ 200A – OA = 350B – OB
= 273.16K – 0K
∴200A = 350B = 273.16K
∴ 1A = \(\frac{273.16}{200}\) K व 1B = \(\frac{273.16}{350}\)
माना कि इन पैमानों पर किसी वस्तु का ताप क्रमश: TA व TB है।
TA = \(\frac{T×273.16}{200}\) K
तथा 1B = \(\frac{T×273.16}{350}\) K
\(\frac{T_{A}}{T_{B}}\) = \(\frac{350}{200}\) = \(\frac{7}{4}\)
TA : TB = 7 : 4
या TA = \(\frac{7}{4}\) TB
प्रश्न 11.3
किसी तापमापी का ओम में विद्युत प्रतिरोध ताप के साथ निम्नलिखित, सन्निकट नियम के अनुसार परिवर्तित होता है –
R = R0 [1 + α (T – T0)]
यदि तापमापी का जल के त्रिक बिन्दु 273.16 K पर प्रतिरोध 101.6 Ω तथा लैड के सामान्य संगलन बिन्दु (600.5 K) पर प्रतिरोध 165.5 Ω है तो वह ताप ज्ञात कीजिए जिस पर तापमापी का प्रतिरोध 123.4 Ω है।
उत्तर:
दिया है:
T1 = 273.16 K पर R1 = 101.612 व T2 = 600.5 K पर R2 = 165.5 माना T0 पर R0 प्रतिरोध है।
तथा T3 ताप पर प्रतिरोध R3 = 123.452 है।
हम जानते हैं कि –
R = R0 [1 + 5 × 10-3 (T – T0)] ……………. (i)
101.6 = R0 [1 + 5 × 10-3(273.16 – T0)] ………………. (ii)
तथा 165.5 = R0 [1 + 5 × 10-3(600.5 – T0)] ………………. (iii)
समी० (iii) को (ii) से भाग देने पर,
\(\frac{165.5}{101.6}\) = \(\frac{1+5 \times 10^{-3}\left(600.5-T_{0}\right)}{1+5 \times 10^{-3}\left(273.16-T_{0}\right)}\)
या 1 + 5 × 10-3(600.5 – T0) = 1.629 [1 + 5 × 10-3 (273.16 – T0)
या 1.629 [1 + 1.366 – 0.005 T0)
= 1 + 3.003 – 0.005 T0
या 3.854 – 008T0 = 4.003 – 0.005T0
या 0.003T0 = -49.67 K
समी० (ii) से,
R0 = \(\frac{101.6}{1+0.005(273.16+49.67)}\)
= \(\frac{101.16}{2.614}\) = 38.87 Ω
123.4 = 38.87 [1 + 0.05) T – (-49.67)]
या T + 49.67 = \(\frac{123.34}{38.87}\) – 1) \(\frac{1}{0.005}\)
या T = 434.94 – 49.67 = 385 K
![]()
प्रश्न 11.4
निम्नलिखित के उत्तर दीजिए –
(a) आधुनिक तापमिति में जल का त्रिक बिन्दु एक मानक नियत बिन्दु है, क्यों? हिम के गलनांक तथा जल के क्वथनांक को मानक नियत-बिन्दु मानने में (जैसा कि मूल सेल्सियस मापक्रम में किया गया था।) क्या दोष है?
(b) जैसा कि ऊपर वर्णन किया जा चुका है कि मूल सेल्सियस मापक्रम में दो नियत बिन्दु थे जिनको क्रमशः 0°C तथा 100°C संख्याएँ निर्धारित की गई थीं। परम ताप मापक्रम पर दो में से एक नियत बिन्दु जल का त्रिक बिन्दु लिया गया है जिसे केल्विन परम ताप मापक्रम पर संख्या 273.16 K निर्धारित की गई है। इस मापक्रम (केल्विन परम ताप) पर अन्य नियत बिन्दु क्या है?
(c) परम ताप (केल्विन मापक्रम) T तथा सेल्सियस मापक्रम पर तापत्र tC में संबंध इस प्रकार है –
tC = T – 273.15 इस संबंध में हमने 273.15 लिखा है 273.16 क्यों नहीं लिखा?
(d) उस परमताप मापक्रम पर, जिसके एकांक अंतराल का आमाप फारेनहाइट के एकांक अंतराल की आमाप के बराबर है, जल के त्रिक बिन्दु का ताप क्या होगा?
उत्तर:
(a) चूँकि जल का त्रिक बिन्दु (273.16 K) एक अद्वितीय बिन्दु है जबकि हिम का गलनांक व जल का क्वथनांक नियत नहीं है। ये दाब परिवर्तित करने पर बदल जाते हैं।
(b) केल्विन मापक्रम पर, 0°C दूसरा नियत बिन्दु परमशून्य ताप है। इस ताप पर सभी गैसों का दाब शून्य हो जाता है।
(c) सेल्सियस पैमाने पर, 0°C ताप सामान्य दाब पर बर्फ का गलनांक है। इसके संगत केल्विन ताप 273.15 K है। अतः प्रत्येक परम ताप (273.16 K), संगत सेल्सियस ताप के 273.15 K ऊँचा है। अतः उक्त सम्बन्ध में 273.15 का प्रयोग किया गया है।
(d) चूँकि 32°F = 273.15 K
तथा 212°F = 373.15 K
∴(212 – 32)°F = (373.15 – 273.15) K
या 180°F = 100K
∴ 1°F = \(\frac{100}{180}\) K
केल्विन मापक्रम में जल के त्रिक बिन्दु का ताप T = 273.16 K
माना नए परमताप पैमाने पर त्रिक बिन्दु का ताप T’ F है।
T’F – 0 F = 273.16 K – 0 K
T’ × \(\frac{100}{180}\) K = 273.16 K
या T = \(\frac{273.16×180}{100}\) = 491.69
अतः नए पैमाने पर त्रिक बिन्दु के ताप का आंकिक मान 491.69 है।
![]()
प्रश्न 11.5
दो आदर्श गैस तापमापियों A तथा B में क्रमश: ऑक्सीजन तथा हाइड्रोजन प्रयोग की गई है। इनके प्रेक्षण निम्नलिखित हैं –
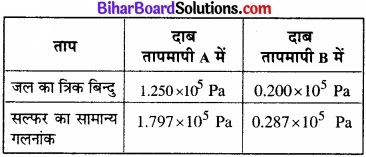
(a) तापमापियों A तथा B के द्वारा लिए गए पाठ्यांकों के अनुसार सल्फर के सामान्य गलनांक के परमताप क्या हैं?
(b) आपके विचार से तापमापियों A तथा B के उत्तरों में थोड़ा अंतर होने का क्या कारण है? (दोनों तापमापियों में कोई दोष नहीं है)। दो पाठ्यांकों के बीच की विसंगति को कम करने के लिए इस प्रयोग में और क्या प्रावधान आवश्यक हैं?
उत्तर:
(a) माना सल्फर का गलनांक T है।
हम जानते हैं कि जल का त्रिक बिन्दु
Ttr = 273.16 K
थर्मामीटर A के लिए
Ptr = 1.250 × 105 Pa,
P = 1.797 × 105 Pa, T = ?
सूत्र \(\frac{T}{T_{\mathrm{tr}}}=\frac{P}{P_{\mathrm{tr}}}\) से
TA = \(\frac{P}{P_{\mathrm{tr}}}\) × Ttr
= \(\frac{1.797 \times 10^{5}}{1.250 \times 10^{5}}\) × 273.16
= 392.69 K
थर्मामीटर B के लिए,
Ptr = 0.200 × 105 Pa
P = 0.287 × 105 Pa
TB = Ttr × \(\frac{P}{P_{\mathrm{tr}}}\)
= 273.16 × \(\frac{0.287 \times 10^{5}}{0.200 \times 10^{5}}\)
या TB = 391.98 K
(b) दोनों तापमापियों के पाठ्यांकों में अन्तर होने का यह कारण है कि प्रयोग की गई गैसें आदर्श नहीं हैं। विसंगति को दूर करने के लिए पाठ्यांक कम दाब पर लेने चाहिए जिससे गैसें आदर्श गैस की भाँति व्यवहार करे।
![]()
प्रश्न 11.6
किसी 1 m लंबे स्टील के फीते का यथार्थ अंशांकन 27.0°C पर किया गया है। किसी तप्त दिन जब ताप 45°C था तब इस फीते से किसी स्टील की छड़ की लंबाई 63.0 cm मापी गई। उस दिन स्टील की छड़ की वास्तविक लंबाई क्या थी? जिस दिन ताप 27.0°C होगा उस दिन इसी छड़ की लंबाई क्या होगी? स्टील का रेखीय प्रसार गुणांक = 1.20 × 10-5 K-1।
उत्तर:
दिया है:
T1 = 27°C पर फीते की लम्बाई, L = 100 सेमी
तथा T2 = 45°C पर फीते द्वारा मापी गई छड़ की ल० l = 63 सेमी।
स्टील का रेखीय प्रसार गुणांक,
α = 1.2 × 10-5 प्रति K
हम जानते हैं कि α = \(\frac{∆L}{L×∆T}\)
L × ∆T × α
= 1000 × (45 – 27) × 1.2 × 10-5
= 0.0216 सेमी
100 सेमी लम्बाई में वृद्धिं = 0.0216 सेमी
1 सेमी लम्बाई में वृद्धि = (0.0216/100) सेमी
63 सेमी लम्बाई में वद्धि = \(\frac{0.0216×63}{100}\)
= 0.0136 सेमी
अत: 45°C ताप पर स्टील की छड़ की वास्तविक लम्बाई
= 63 + 0.0136 सेमी।
= 63.0136 सेमी।
तथा जिस दिन ताप 27°C है उस दिन पुन: स्टील की छड़ की लम्बाई 63.0136 सेमी होगी।
![]()
प्रश्न 11.7
किसी बड़े स्टील के पहिए को उसी पदार्थ की किसी धुरी पर ठीक बैठाना है। 27°C पर धुरी का बाहरी व्यास 8.70 cm तथा पहिए के केंद्रीय छिद्र का व्यास 8.69 cm है। सूखी बर्फ द्वारा धुरी को ठंडा किया गया है। धुरी के किस ताप पर पहिया धुरी पर चढ़ेगा? यह मानिए कि आवश्यक ताप परिसर में स्टील का रैखिक प्रसार गुणांक नियत रहता है –
α स्टील = 1.2 × 10-5 K-1
उत्तर:
माना कि T1 व T2 पर स्टील की रैखिक माप क्रमश: l1 व l2 है।
दिया है: αsteel = 1.20 × 10-5 K-1
l1 = 8.70 cm
l2 = 8.69 cm
T1 = 27°C = 273 + 27 = 300 K
T2 = ?
स्टील की शॉफ्ट को ठण्डा करने पर, लम्बाई निम्नवत् होती है –
l2 = l1 [1 + α(T2 – T1)] …………… (1)
शॉफ्ट को T2 ताप पर ठण्डा करने पर l2 = 8.69 सेमी०, तब पहिया शॉफ्ट पर फिसल सकेगा।
अतः समी० (1) से,
8.69 = 8.70 [1 + 1.20 × T-5(T2 – 300)]
या T2 – 300 = \(\frac{8.69-8.70}{8.70 \times 1.20 \times 10^{-5}}\)
= -95.78 K
या T2 = 300 – 95.78 = 204.22 K
या = 204.22 – 273.15 = -68.93°C
= -68.93°C
या T2 = -69°C
![]()
प्रश्न 11.8
ताँबे की चादर में एक छिद्र किया गया है। 27.0°C पर छिद्र का व्यास 4.24 cm है। इस धातु की चादर को 227°C तक तप्त करने पर छिद्र के व्यास में क्या परिवर्तन होगा? ताँबे का रेखीय प्रसार गुणांक = 1.70 × 10-5 K-1।
उत्तर:
दिया है:
t1 = 27°C
t2 = 227°C
∆t = 227 – 27 = 200°C
ताँबे के लिए रेखीय प्रसार गुणांक
α = 1.7 × 10-5°C-1
27°C पर छिद्र का व्यास, d1 = 4.24 सेमी
माना कि 227°C पर छिद्र का व्यास = d2
∆d = d2 – d1 = ?
ताँबे के लिए क्षेत्रीय प्रसार गुणांक
β = 2a = 2 × 1.7 × 10-5
= 3.4 × 10-5°C-1
माना छिद्र का पृष्ठ क्षेत्रफल 27°C व 227°C पर क्रमश: S1 व S2 है।
S1 = \(\frac{\pi d_{1}^{2}}{4}\) = \(\frac{π}{4}\) × (4.24)2
= 4.4947 π सेमी2
S2 = S1 (1 + β ∆t)
= 4.49π (1 + 3.40 × 10-5 × 200)
या S2 = 4.49π × 1.00668
= 4.525 πcm2
या \(\frac{\pi d_{2}^{2}}{4}\) = 4.25π
या d2 = \(\sqrt{4.525×4}\) = 4.525 cm
∆d = d2 – d1 = 4.2544 cm
= 0.0144 cm
या ∆d = 1.44 × 10-2 सेमी
![]()
प्रश्न 11.9
27°C पर 1.8 cm लंबे किसी ताँबे के तार को दो दृढ़ टेकों के बीच अल्प तनाव रखकर थोड़ा कसा गया है। यदि तार को -39°C ताप पर शीतित करें तो तार में कितना तनाव उत्पन्न हो जाएगा? तार का व्यास 2.0 mm है। पीतल का रेखीय प्रसार गुणांक = 2.0 × 10-5K-1 पीतल का यंग प्रत्यास्थता गुणांक = 0.91 × 1011Pa
उत्तर:
दिया है:
l1 = 1.8 m, t1 = 27°C, t2 = -39°C
∆t = t2 – t1
= – 39 – 27
= -66°C t2°C पर लम्बाई = l2
पीतल के लिए α = 2 × 10-50 K-1
Y = 0.91 × 1011 Pa
तार का व्यास
d = 2.0 mm
= 2.0 × 10-3 m
माना तार का अनुप्रस्थ परिच्छेद a है।
a = \(\frac{\pi d^{2}}{4}\) = \(\frac{π}{4}\) × (2.0 × 10-3)2
= 3.142 × 10-6 m2
माना तार में उत्पन्न तनाव F है।
अतः सूत्र Y = \(\frac{F/a}{∆l/L}\) से
F = \(\frac{Y a \Delta l}{l_{1}}\) ………………. (i)
परन्तु l = l1 α ∆t
= 1.8 × 2 × 10-5 × (-66)
= -0.00237 m
= -0.0024 m
ऋणात्मक चिह्न प्रदर्शित करता है कि समी० (i) में Y, a, ∆l तथा l1 का मान रखने पर लम्बाई घटती है।

= 381N
= 3.81 × 102 N
![]()
प्रश्न 11.10
50 cm लंबी तथा 3.00 mm व्यास की किसी पीतल की छड़ को उसी लंबाई तथा व्यास की किसी स्टील की छड़ से जोड़ा गया है। यदि ये मूल लंबाइयाँ 40°C पर हैं, तो 250°C पर संयुक्त छड़ की लंबाई में क्या परिवर्तन होगा? क्या संधि पर कोई तापीय प्रतिबल उत्पन्न होगा? छड़ के सिरों को प्रसार के लिए मुक्त रखा गया है। (पीतल तथा स्टील के रेखीय प्रसार गुणांक क्रमशः = 2.0 × 10-5 K-1, स्टील = 1.2 × 10-5 K-1 हैं।)
उत्तर:
पीतल की छड़ के लिए,
α = 2.0 × 10-5 K-1, l1 = 50 cm, t1 = 40°C
t2 = 250°C
∆t = t2 – t1
= 250 – 40 = 210°C
माना t2°C पर लम्बाई l2 है। अतः
l2 = l1(1 + α ∆t)
= 50 (1 + 2 × 10-5 × 210)
= 50.21 cm
∆l brass = l2 – l1
= 50.21 – 50
= 0.21 cm
स्टील की छड़ के लिए,
t1 = 40°C, t2 = 250°C, α = 1.2 × 10-5 K-1,
l1 = 50.0 cm
∆t’ = t2 – t1
= 250 – 40 = 210°C
माना 250°C पर स्टील छड़ की ल० l2 है
अतः l2 = l1 (1 + α ∆t’)
= 50 (1 + 1.2 × 10-5 × 210)
= 50.126 cm
250°C पर संयुक्त छड़ की लम्बाई 250°C = l2 + l2
= 50.21 + 50.126
= 100.336 cm व 40°C पर संयुक्त छड़ की लम्बाई
= l1 + l1 = 50 + 50
= 100 cm
संयुक्त छड़ की लम्बाई में परिवर्तन
= 100.336 – 100
= 0.336 cm
= 0.34 cm
अतः सन्धि पर कोई तापीय प्रतिबल उत्पन्न नहीं होता है।
![]()
प्रश्न 11.11
ग्लिसरीन का आयतन प्रसार गुणांक 4.9 × 10-5 K-1 है। ताप में 30°C की वृद्धि होने पर इसके घनत्व में क्या आंशिक परिवर्तन होगा?
उत्तर:
दिया है:
V = 4.9 × 10-5 K-1
ताप में वृद्धि ∆t = 30°C
माना 0°C पर ग्लिसरीन का प्रा० आयतन V0 है।
माना 30°C पर ग्लिसरीन का आयतन V1 है।
तब V1 = v0 (1 + r ∆t)
= V0(1 + 49 × 10-5 × 30)
= V0(1 + 0.01470)
= 1.01470 V0
या \(\frac{V_{0}}{V_{1}}\) = \(\frac{1}{1.01470}\) ……………….. (i)
अतः प्रारम्भिक घनत्व, P0 = \(\frac{m}{V_{0}}\)
तथा अन्तिम घनत्व, P1 = \(\frac{m}{V_{t}}\)
जहाँ m ग्लिसरीन का द्रव्यमान है।
\(\frac{\Delta \rho}{\rho_{0}}\) = घनत्व में भिन्नात्मक परिवर्तन

यहाँ गुणात्मक चिह्न प्रदर्शित करता है कि ताप में वृद्धि से घनत्व घटता है।
\(\frac{\Delta \rho}{\rho_{0}}\) = 0.0145 = 1.45 × 10-2
= -1.5 × 10-2
![]()
प्रश्न 11.12
8.0 kg द्रव्यमान के किसी एल्युमीनियम के छोटे ब्लॉक में छिद्र करने के लिए किसी 10 W की बरमी का उपयोग किया गया है। 2.5 मिनट में ब्लॉक के ताप में कितनी वृद्धि हो जाएगी। यह मानिए कि 50% शक्ति तो स्वयं बरमी को गर्म करने में खर्च हो जाती है अथवा परिवेश में लुप्त हो जाती है। एल्युमीनियम की विशिष्ट ऊष्मा धारिता = 0.91Jg-1 K-1 है।
उत्तर:
दिया है:
m = 8 kg
शक्ति, P = 10 KW = 10 × 103 J/S
समय t = 2.5 मिनट = 150 सेकण्ड
विशिष्ट ऊष्मा धारिता S = 0.91 Jg-1 K-1
= 910 Jkg-1 K-1
2.5 मिनट में बमों द्वारा कम की गई ऊर्जा, E = Pt
= (10 × 103) × 150
= 1.5 × 106 जूल
माना सम्पूर्ण ऊर्जा ऊष्मा में परिवर्तित हो जाती है जिसका 50% बर्मे द्वारा अवशोषित हो जाता है।
अतः ब्लॉक द्वारा शोषित ऊष्मा,
θ = E का 50%
= 1.5 × 106 × \(\frac{50}{100}\)
= 1.5 × 106 जूल
माना शोषित ऊष्मा से ब्लॉक के ताप में वृद्धि ∆T है।
सूत्र θ = ms ∆T से,
∆T = \(\frac{θ}{ms}\) = \(\frac{0.75 \times 10^{-6}}{8 \times 910}\)
= 103°C
![]()
प्रश्न 11.13
2.5 kg द्रव्यमान के ताँबे के गुटके को किसी भट्टी में 500°C तक तप्त करने के पश्चात् किसी बड़े हिम-ब्लॉक पर रख दिया जाता है। गलित हो सकने वाली हिम की अधिकतम मात्रा क्या है? ताँबे की विशिष्ट ऊष्मा धारिता = 0.39Jg-1 K-1; बर्फ की संगलन ऊष्मा = 335 Jg-1
उत्तर:
दिया है:
m = 2.5 kg
T1 = 500°C विशिष्ट ऊष्मा धारिता,
S = 0.39 Jg-1 K-1 = 390 Jkg-1 K-1
बर्फ की संगलन ऊष्मा,
Lf = 335 Jg-1
= 335 × 103 Jkg-1
प्रश्नानुसार, निकाय का अन्तिम ताप T2 = 0°C
∆T = T1 – T2
= 500°C या 500 K
सूत्र θ = ms ∆T से
गुट के द्वारा दी गई ऊष्मा,
θ = 2.5 × 390 × 500
= 48.75 × 107 J
माना कि बर्फ का m’ द्रव्यमान इस ऊष्मा को शोषित कर गल जाता है।
Q = m’Lf
m’ = \(\frac{\theta}{L_{f}}\)
= \(\frac{48.75 \times 10^{4}}{335 \times 10^{3}}\) = 1.45 kg
![]()
प्रश्न 11.14
किसी धातु की विशिष्ट ऊष्मा धारिता के प्रयोग में 0.20 kg के धातु के गुटके को 150°C पर तप्त करके, किसी ताँबे के ऊष्मामापी (जल तुल्यांक 30.025 kg), जिसमें 27°C का 150 cm3 जल भरा है, में गिराया जाता है। अंतिम ताप 40°C है। धातु की विशिष्ट ऊष्मा धारिता परिकलित कीजिए। यदि परिवेश में क्षय ऊष्मा उपेक्षणीय न मानकर परिकलन किया जाता है, तब क्या आपका उत्तर धातु की विशिष्ट ऊष्मा धारिता के वास्तविक मान से अधिक मान दर्शाएगा अथवा कम?
उत्तर:
दिया है:
गुटके का द्रव्यमान m = 0.20 kg
ऊष्मामापी का जल तुल्यांक m1 = 0.025 kg
भरे जल का द्रव्यमान m2 = 150 gm = 0.15 kg
गुटके का प्रारम्भिक ताप Ti = 150°C
ऊष्मामापी तथा जल का प्रारम्भिक ताप T’i = 27°C
मिश्रण का ताप, Tf = 40°C
![]()
माना धातु की विशिष्ट ऊष्मा धारिता Sm है।
गुटके द्वारा दी गई ऊष्मा,
Q = ms(Ti – Tf)
तथा ऊष्मामापी व जल द्वारा ली गई ऊष्मा
![]()
परन्तु दी गई ऊष्मा = ली गई ऊष्मा

यदि हम परिवेश में ऊष्मा क्षय को नगण्य न मानकर परिकलित करें, तब उपरोक्त मान वास्तविक विशिष्ट ऊष्मा धारिता से कम मान दर्शाएगा।
![]()
प्रश्न 11.15
कुछ सामान्य गैसों के कक्ष ताप पर मोलर विशिष्ट ऊष्मा धारिताओं के प्रेक्षण नीचे दिए गए हैं –
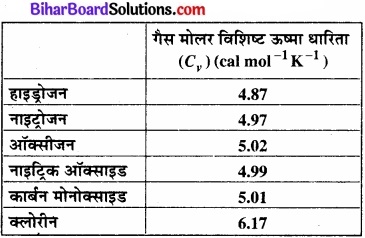
इन गैसों की मापी गई मोलर विशिष्ट ऊष्मा धारिताएँ एक परमाणुक गैसों की मोलर विशिष्ट ऊष्मा धारिताओं से सुस्पष्ट रूप से भिन्न हैं। प्रतीकात्मक रूप में किसी एक परमाणुक गैस की मोलर विशिष्ट ऊष्मा धारिता 2.92 cal/mol K होती है। इस अंतर का स्पष्टीकरण कीजिए। क्लोरीन के लिए कुछ अधिक मान (शेष की अपेक्षा) होने से आप क्या निष्कर्ष निकालते हैं?
उत्तर:
एक परमाणुक गैसों के अणुओं में सिर्फ स्थानान्तरीय गतिज ऊर्जा होती है परन्तु द्विपरमाणुक गैसों के अणुओं में स्थानान्तरीय गतिज ऊर्जा के अतिरिक्त घूर्णी गतिज ऊर्जा भी होती है। इसका कारण यह है कि द्विपरमाणुक गैसों के अणु अन्तराण्विक अक्ष के लम्बवत् दो अक्षों के परितः भी घूर्णन कर सकते हैं।
किसी गैस को ऊष्मा देने पर यह ऊष्मा अणुओं की सभी प्रकार की भुजाओं में समान वृद्धियाँ करती हैं। चूँकि द्विपरमाणुक गैसों के अणुओं की ऊर्जा के प्रकार अधिक होते हैं इसलिए इनकी मोलर विशिष्ट ऊष्मा धारिताएँ भी अधिक होती हैं। क्लोरीन की मोलर विशिष्ट ऊष्मा धारिता का अधिक मान यह व्यक्त करता है कि इसके अणु स्थानान्तरीय व घूर्णनी गतिज ऊर्जा के अतिरिक्त काम्पनिक गतिज ऊर्जा भी रखते हैं।
प्रश्न 11.16
101°F ताप ज्वर से पीड़ित किसी बच्चे को एन्टीपायरिन ( ज्वर कम करने की दवा) दी गई जिसके कारण उसके शरीर से पसीने के वाष्पन की दर में वृद्धि हो गई। यदि 20 मिनट में ज्वर 98°F तक गिर जाता है तो दवा द्वारा होने वाले अतिरिक्त वाष्पन की औसत दर क्या है? यह मानिए कि ऊष्मा ह्रास का एकमात्र उपाय वाष्पन ही है। बच्चे का द्रव्यमान 30 kg है। मानव शरीर की विशिष्ट ऊष्मा धारिता जल की विशिष्ट ऊष्मा धारिता के लगभग बराबर है तथा उस ताप पर जल के वाष्पन की गुप्त ऊष्मा 580 cal g-1 है।
उत्तर:
दिया है:
बच्चे का द्रव्यमान, m = 30 kg
ताप में गिरावट, ∆T = T1 – T2
= 101°F – 98°F
= 3°F = 3 × \(\frac{5}{9}\)°C
या ∆T = \(\frac{5}{3}\)°C
मानव शरीर की विशिष्ट ऊष्मा
C = 4.2 × 103 Jkg-1C-1
वाष्पन की गुप्त ऊष्मा = 580 cal g-1
= 580 × 4.2 × 103 Jkg-1C-1
माना 20 मिनट में बच्चे के शरीर से m ग्राम पसीना उत्सर्जित होता है।
माना आवश्यक ऊष्मा Q है।
अतः Q = m’L
= m × 580 × 4.2 × 103 J ……………. (i)
माना पसीने के उत्सर्जन के रूप में ऊष्मा Q का ह्रास होता है।
अतः Q = mCAT
= 30 × 4.2 × 103 × 51
= 2.10 × 105 J ………………. (ii)
समी० (i) व (ii) से,
m’ × 580 × 4.2 × 103
= 2.1 x 105
या m’ = \(\frac{2.1 \times 10^{5}}{580 \times 4.2 \times 10^{3}}\)
= \(\frac{10}{116}\) = 0.0862 kg
पसीने के उत्सर्जित होने की दर
= \(\frac{m’}{t}\) = \(\frac{0.0862}{20}\)
= 0.00431 kg min-1 = 4.31 g min-1
![]()
प्रश्न 11.17
थर्मोकोल का बना ‘हिम बॉक्स’ विशेषकर गर्मियों में कम मात्रा के पके भोजन के भंडारण का सस्ता तथा दक्ष साधन है। 30 cm भुजा के किसी हिम बॉक्स की मोटाई 5.0 cm है। यदि इस बॉक्स में 4.0 kg हिम रखा है तो 6 h के पश्चात् बचे हिम की मात्रा का आंकलन कीजिए। बाहरी ताप 45°C है तथा थर्मोकोल की ऊष्मा चालकता 0.01 Js-1 m-1 K-1 है। (हिम की संगलन ऊष्मा = 335 × 103 Jkg-1)
उत्तर:
दिया है:
घन के छह पृष्ठों का क्षेत्रफल
= 6 × 30 × 30 cm2
= 6 × 900 × 10-4 m2
दूरी, d = 5.0 cm = 5.0 × 10-2 m
बर्फ का कुल द्रव्यमान, M = 4 kg
समय t = 6 h = 6 × 60 × 60s
बक्से के बाहर का ताप = Q1 = 45°C
बक्से के भीतर का ताप = Q2 = 0°C
∆θ = θ1 – θ1 = 45 – 0
= 45°C
संगलन की ऊष्मा,
L = 335 × 103 Jkg-1
थर्माकोल की ऊष्मीय चालकता गुणांक
= K = 0.01 Js-1 m-10 K-1
माना बर्फ का m kg द्रव्यमान गलता है
अतः 0°C पर गलन के लिए आवश्यक ऊष्मा,
Q = mL ……………. (i)
पुनः Q = KA \(\frac{∆θ}{d}\) t ……………… (ii)
समी० (i) व (ii) से,
m = \(\frac{KA}{L}\) \(\frac{∆θ}{d}\) t

= 0.313 kg
बॉक्स में शेष बची हिम का द्रव्यमान = M – m
= 4 – 0.313
= 3.687
= 3.7 किग्रा
![]()
प्रश्न 11.18
किसी पीतल के बॉयलर की पेंदी का क्षेत्रफल 0.15 m2 तथा मोटाई 1.0 cm है। किसी गैस स्टोव पर रखने पर इसमें 6.0 kg/min की दर से जल उबलता है। बॉयलर के संपर्क की ज्वाला के भाग का ताप आकलित कीजिए। पीतल की ऊष्मा चालकता = 109 Js-1 m-1 K-1; जल की वाष्पन ऊष्मा = 2256 × 103 Jkg-1 है।
उत्तर:
दिया है:
K = 109 Js-1 m-1 K-1
A = 0.15 m2
d = 1.0 cm = 10-2 m θ2 = 100°C
माना बॉयलर के स्टोव के सम्पर्क वाले हिस्से का ताप θ1 है।
अत: Q = \(\frac{K A\left(\theta_{1}-\theta_{2}\right)}{d}\)
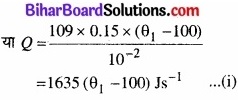
जल के, वाष्पीकरण की ऊष्मा,
L = 2256 × 103 Jkg-1
बॉयलर में जल के उबलने की दर,
M = 6.0 kg min-1
= \(\frac{6.0}{60}\) = 0.1 kg-1 s
जल द्वारा प्रति सेकण्ड अवशोषित ऊष्मा, Q = ML
या Q = 0.1 × 2256 × 103 Js-1
समी० (i) व (ii) से
1635 (θ1 – 100) = 2256 × 102
या θ1 – 100 = \(\frac{2256×100}{1635}\) = 138
θ1 = 100 + 138 = 238°C
![]()
प्रश्न 11.19
स्पष्ट कीजिए कि क्यों –
(a) अधिक परावर्तकता वाले पिंड अल्प उत्सर्जक होते हैं।
(b) कँपकँपी वाले दिन लकड़ी की ट्रे की अपेक्षा पीतल का गिलास कहीं अधिक शीतल प्रतीत होता है।
(c) कोई प्रकाशिक उत्तापमापी ( उच्च तापों को मापने की युक्ति), जिसका अंशांकन किसी आदर्श कृष्णिका के विकिरणों के लिए किया गया है,खुले में रखे किसी लाल तप्त लोहे के टुकड़े का ताप काफी कम मापता है, परन्तु जब उसी लोहे के टुकड़े को भट्टी में रखते हैं, तो वह ताप का सही मान मापता है।
(d) बिना वातावरण के पृथ्वी अशरणीय शीतल हो जाएगी।
(e) भाप के परिचालन पर आधारित तापन निकाय तप्त जल के परिचालन पर आधारित निकायों की अपेक्षा भवनों को उष्ण बनाने में अधिक दक्ष होते हैं।
उत्तर:
(a) चूँकि उच्च परावर्तकता वाले पिंड अपने ऊपर गिरने वाले अधिकांश विकिरण को परावर्तित कर देते हैं। अतः वे अल्प अवशोषक होते हैं। इसी कारण वे अल्प उत्सर्जक भी होते हैं।
(b) लकड़ी की ट्रे ऊष्मा की कुचालक होती है तथा पीतल का गिलास ऊष्मा का सुचालक होता है। कँपकँपी वाले दिन दोनों ही समान ताप पर होंगे। लेकिन स्पर्श करने पर गिलास हमारे हाथ से तेजी से ऊष्मा लेता है जबकि लकड़ी की ट्रे बहुत कम ऊष्मा लेती है। अतः गिलास ट्रे की तुलना में अधिक ठण्डा लगता है।
(c) चूँकि खुले में रखे तप्त लोहे का गोला तीव्रता से ऊष्मा खोता है तथा कम ऊष्माधारिता के कारण तीव्रता से ठण्डा होता जाता है। इस प्रकार उत्तापमापी को पर्याप्त विकिरण ऊर्जा लगातार नहीं मिल पाती है। जबकि भट्टी में रखने पर, गोले का ताप स्थिर बना रहता है तथा यह नियत दर से विकिरण उत्सर्जित करता है।
(d) चूँकि वायु ऊष्मा की कुचालक है। अतः पृथ्वी के चारों ओर का वायुमण्डल एक कम्बल की तरह व्यवहार करता है तथा पृथ्वी से उत्सर्जित होने वाले ऊष्मीय विकिरणों को वापस पृथ्वी की ओर को परावर्तित करता है। वायुमण्डल की अनुपस्थिति में, पृथ्वी से उत्सर्जित होने वाले ऊष्मीय विकिरण सीधे सुदूर अन्तरिक्ष में चले जाते हैं। एवम् पृथ्वी अशरणीय शीतल हो जाएगी।
(e) चूँकि 1 g जलवाष्प, 100°C के 1 g जल की तुलना में 540 cal अतिरिक्त ऊष्मा रखती है। अतः स्पष्ट है कि जलवाष्प आधारित तापन निकाय, तप्त जल आधारित तापन निकाय से ज्यादा दक्ष है।
![]()
प्रश्न 11.20
किसी पिंड का ताप 5 मिनट में 80°C से 50°C हो जाता है। यदि परिवेश का ताप 20°C है, तो उस समय का परिकलन कीजिए जिसमें उसका ताप 60°C से 30°C हो जाएगा।
उत्तर:
80°C व 50°C का माध्य ताप 65°C है।
अतः परिवेश ताप से अन्तर = (65 – 20) = 45°C
सूत्र ताप में कमी/समयान्तराल = K (तापान्तर) से …………… (i)
60°C व 30° C का माध्य ताप 45°C है।
इसका परिवेश ताप से अन्तर (45 – 20) = 25°C
या t = \(\frac{30}{6}\) × \(\frac{45}{25}\) = 9 मिनट
अतः पिंड के ताप को 60°C से 30°C तक गिरने में 9 मिनट लगते हैं।
Bihar Board Class 11 Physics द्रव्य के तापीय गुण Additional Important Questions and Answers
अतिरिक्त अभ्यास के प्रश्न एवं उनके उत्तर
प्रश्न 11.21
CO2 के P – T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) किस ताप व दाब पर CO2 की ठोस, द्रव तथा वाष्प प्रावस्थाएँ साम्य में सहवर्ती हो सकती हैं?
(b) CO2 के गलनांक तथा क्वथनांक पर दाब में कमी का क्या प्रभाव पड़ता है?
(c) CO2 के लिए क्रांतिक ताप तथा दाब क्या हैं? इनका क्या महत्व है?
(d)
- -70°C ताप व 1 atm दाब
- -60°Cताप व 10atm दाब
- 15°C ताप व 56 atm दाब पर CO2 ठोस, द्रव अथवा गैस में से किस अवस्था में होती है?
उत्तर:
(a) -56.6°C ताप व 5.11 वायुमण्डलीय दाब पर।
(b) दाब में कमी होने पर दोनों घटते हैं।
(c) CO2 के लिए क्रान्तिक ताप 31.1°C व क्रान्तिक दाब 73 वायुमण्डलीय दाब है।
(d)
- – 70°C ताप व 1 atm दाब पर वाष्प या गैसीय अवस्था में।
- – 60°C ताप व 10 atm दाब पर ठोस अवस्था में।
- 15°C ताप व 56 atm दाब पर द्रव अवस्था में।
![]()
प्रश्न 11.22
CO2 के P – T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए –
(a) 1 atm दाब तथा – 60°Cताप पर CO2 का समतापी संपीडन किया जाता है? क्या यह द्रव प्रावस्था में जाएगी?
(b) क्या होता है जब 4atm दाब व CO2 का दाब नियत रखकर कक्ष ताप पर शीतन किया जाता है?
(c) 10 atm दाब तथा -65°C ताप पर किसी दिए गए द्रव्यमान की ठोस CO2 को दाब नियत रखकर कक्ष ताप तक तप्त करते समय होने वाले गुणात्मक परिवर्तनों का वर्णन कीजिए।
(d) CO2 को 70°C तक तप्त तथा समतापी संपीडित किया जाता है। आप प्रेक्षण के लिए इसके किन गुणों में अंतर की अपेक्षा करते हैं?
उत्तर:
(a) समतापी सम्पीडनं से तात्पर्य है कि गैस को – 60°C ताप पर दाब अक्ष के समान्तर ऊपर को ले जाया जाता है। इसके लिए हम (- 60°C) ताप पर दाब अक्ष के समान्तर रेखा खींचते हैं। यह रेखा गैसीय क्षेत्र से सीधे ठोस क्षेत्र में प्रवेश कर जाती है तथा द्रव क्षेत्र से नहीं जाती है। अर्थात् गैस बिना द्रवित हुए ठोस में परिवर्तित हो जाती है।
(b) यहाँ पर 4 atm दाब पर ताप अक्ष के समान्तर रेखा खींचते हैं। हम देखते हैं कि यहाँ रेखा वाष्प क्षेत्र से सीधे ठोस क्षेत्रों में प्रवेश करती है। इसका तात्पर्य है कि गैस, बिना द्रवित हुए ठोस अवस्था में संघनित होगी।
(c) यहाँ हम 10 atm दाब व – 65°C ताप से प्रारम्भ कर ताप अक्ष के समान्तर रेखा खींचते हैं। यह रेखा ठोस क्षेत्र से द्रव क्षेत्र तथा बाद में वाष्प क्षेत्र में प्रवेश करती है। इसका तात्पर्य यह है कि इस ताप व दाब पर गैस ठोस अवस्था में होगी। गर्म करने पर यह गैस धीरे-धीरे द्रवास्था में आ जाएगी व पुनः गर्म करने पर गैसीय अवस्था में आ जाएगी।
(d) चूँकि 70°C ताप गैस के क्रान्ति ताप से अधिक है। अतः इसे समतापी सम्पीडन से द्रवित नहीं किया जा सकता है। इस प्रकार चिर स्थायी गैसों की भाँति दाब बढ़ाते जाने पर इसका आयतन कम होता जाएगा।