Bihar Board 12th Maths Objective Answers Chapter 3 Matrices

Bihar Board 12th Maths Objective Questions and Answers

Bihar Board 12th Maths Objective Answers Chapter 3 Matrices

Question 1.

Answer:
(b) \(\left[\begin{array}{ccc}
0 & -1 / 3 & -1 / 2 \\
1 / 3 & 0 & -1 / 5 \\
1 / 2 & 1 / 5 & 0 \\
3 / 5 & 1 / 3 & 1 / 7
\end{array}\right]\)

Question 2.
The matrix A = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) is a
(a) unit matrix
(c) symmetric matrix
(b) diagonal matrix
(d) skew-symmetric matrix
Answer:
(d) skew-symmetric matrix

Question 3.
If \(\left[\begin{array}{cc}
x+y & 2 x+z \\
x-y & 2 z+w
\end{array}\right]=\left[\begin{array}{cc}
4 & 7 \\
0 & 10
\end{array}\right]\), then the values of x, y, z and w respectively are
(a) 2, 2, 3, 4
(b) 2, 3, 1, 2
(c) 3, 3, 0, 1
(d) None of these
Answer:
(a) 2, 2, 3, 4

Question 4.
then find the values of a, b, c, x, y and z respectively
(a) -2, -7, -1, -3, -5, 2
(b) 2, 7, 1, 3, 5, -2
(c) 1, 3, 4, 2, 8, 9
(d) -1, 3, -2, -7, 4, 5
Answer:
(a) -2, -7, -1, -3, -5, 2

Question 5.
The order of the single matrix obtained from

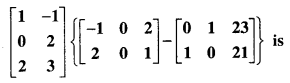
(a) 2 × 3
(b) 2 × 2
(c) 3 × 2
(d) 3 × 3
Answer:
(d) 3 × 3

Question 6.
\(A=\left[\begin{array}{ll}
1 & -1 \\
2 & -1
\end{array}\right], B=\left[\begin{array}{ll}
x & 1 \\
y & -1
\end{array}\right]\) and (A + B)² = A² + B², then x + y =
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(d) 5

Question 7.
If A = \(\left[\begin{array}{lll}
2 & 2 & 1 \\
1 & 3 & 1 \\
1 & 2 & 2
\end{array}\right]\), then A⁴ – 2⁴ (A – I) =
(a) 5I + A
(b) 5I – A
(c) 5I
(d) 6I
Answer:
(b) 5I – A

Question 8.
If A is an m × n matrix such that AB and BA are both defined, then B is a
(a) m × n matrix
(b) n × m matrix
(c) n × n matrix
(d) m × n matrix
Answer:
(b) n × m matrix

Question 9.
If \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\), then A² – 5A is equal to
(a) 2I
(b) 3I
(c) -2I
(d) null matrix
Answer:
(a) 2I

Question 10.

(a) A + B = B + A and A + (B + C) = (A + B) + C
(b) A + B = B + A and AC = BC
(c) A + B = B + A and AB = BC
(d) AC = BC and A = BC
Answer:
(a) A + B = B + A and A + (B + C) = (A + B) + C

Question 11.

(a) α = a² + b², β = ab
(b) α = a² + b², β = 2ab
(c) α = a² + b², β = a² – b²
(d) α = 2ab, β = a² + b²
Answer:
(b) α = a² + b², β = 2ab

Question 12.
If A = \(\left[\begin{array}{lll}
1 & 2 & x \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & -2 & y \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) and AB = I₃, then x + y equals
(a) 0
(b) -1
(c) 2
(d) None of these
Answer:
(a) 0

Question 13.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 1
\end{array}\right]\) and f(x) = (1 + x) (1 – x), then f(a) is

Answer:
(a) \(-4\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)

Question 14.
If A = \(\left[\begin{array}{ll}
1 & 3 \\
3 & 4
\end{array}\right]\) and A² – KA – 5I = 0, then K =
(a) 5
(b) 3
(c) 7
(d) None of these
Answer:
(a) 5

Question 15.

Answer:
(b) \(\left[\begin{array}{cc}
-3 & 10 \\
-2 & 7
\end{array}\right]\)

Question 16.
If matrix A = \(\left[\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right]\) where a, b, c are real positivenumbers, abc = 1 and A^TA = I, then the value of a³ + b³ + c³ is
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 17.
Find the values of x, y, z respectively if the matrix \(A=\left[\begin{array}{ccc}
0 & 2 y & z \\
x & y & -z \\
x & -y & z
\end{array}\right]\) satisfy the equation A^TA = I₃.
(a) \(\frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{6}}, \frac{1}{\sqrt{3}}\)
(b) \(\frac{-1}{\sqrt{2}}, \frac{-1}{\sqrt{6}}, \frac{-1}{\sqrt{3}}\)
(c) Both (a) and (b)
(d) None of these
Answer:
(c) Both (a) and (b)

Question 18.
If \(A=\left[\begin{array}{cc}
\cos x & -\sin x \\
\sin x & \cos x
\end{array}\right]\), find AAT.
(a) Zero Matrix
(b) I₂
(c) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
(d) None of these
Answer:
(b) I₂

Question 19.
If \(A=\left[\begin{array}{ccc}
0 & -1 & 2 \\
1 & 0 & 3 \\
-2 & -3 & 0
\end{array}\right]\), then A + 2A^T equals
(a) A
(b) -A^T
(c) A^T
(d) 2A²
Answer:
(c) A^T

Question 20.
For any square matrix A, AA^T is a
(a) unit matrix
(b) symmetric matrix
(c) skew-symmetric matrix
(d) diagonal matrix
Answer:
(b) symmetric matrix

Question 21.
If A and B are symmetric matrices of the same order, then
(a) AB is a symmetric matrix
(b) A – Bis askew-symmetric matrix
(c) AB + BA is a symmetric matrix
(d) AB – BA is a symmetric matrix
Answer:
(c) AB + BA is a symmetric matrix

Question 22.
If \(A=\left[\begin{array}{cc}
3 & x-1 \\
2 x+3 & x+2
\end{array}\right]\) is a symmetric matrix, then x =
(a) 4
(b) 3
(c) -4
(d) -3
Answer:
(c) -4

Question 23.
If A is a square matrix, then A – A’ is a
(a) diagonal matrix
(b) skew-symmetric matrix
(c) symmetric matrix
(d) none of these
Answer:
(b) skew-symmetric matrix

Question 24.
If A is any square matrix, then which of the following is skew-symmetric?
(a) A + A^T
(b) A – A^T
(c) AA^T
(d) A^TA
Answer:
(b) A – A^T

Question 25.
If A = \(\left[\begin{array}{lll}
6 & 8 & 5 \\
4 & 2 & 3 \\
9 & 7 & 1
\end{array}\right]\) is the sum of a symmetric matrix B and skew-symmetric matrix C, then B is

Answer:
(a) \(A=\left[\begin{array}{lll}
6 & 6 & 7 \\
6 & 2 & 5 \\
7 & 5 & 1
\end{array}\right]\)

Question 26.
If the matrix A = \(\left[\begin{array}{ccc}
5 & 2 & x \\
y & 2 & -3 \\
4 & t & -7
\end{array}\right]\) is a symmetric matrix, then find the value of x, y and t respectively.
(a) 4, 2, 3
(b) 4, 2, -3
(c) 4, 2, -7
(d) 2, 4, -7
Answer:
(b) 4, 2, -3

Question 27.
If a matrix A is both symmetric and skew-symmetric, then
(a) A is a diagonal matrix
(b) A is a zero matrix
(c) A is a scalar matrix
(d) A is a square matrix
Answer:
(b) A is a zero matrix

Question 28.
The matrix \(\left[\begin{array}{ccc}
0 & 5 & -7 \\
-5 & 0 & 11 \\
7 & -11 & 0
\end{array}\right]\) is
(a) a skew-symmetric matrix
(b) a symmetric matrix
(c) a diagonal matrix
(d) an upper triangular matrix
Answer:
(a) a skew-symmetric matrix

Direction (29 – 31): Find the inverse of each of the following matrices by using elementary row transformations.

Question 29.

Answer:
(a) \(\frac{1}{13}\left[\begin{array}{ccc}
-1 & 3 & -3 \\
5 & -2 & 15 \\
5 & -2 & 2
\end{array}\right]\)

Question 30.

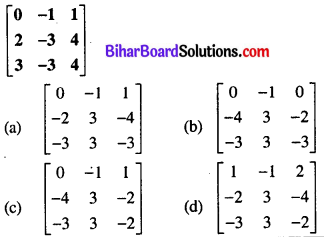
Answer:
(c) \(\left[\begin{array}{ccc}
0 & -1 & 1 \\
-4 & 3 & -2 \\
-3 & 3 & -2
\end{array}\right]\)

Question 31.

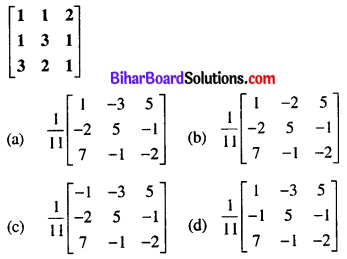
Answer:
(c) \(\frac{1}{11}\left[\begin{array}{ccc}
-1 & -3 & 5 \\
-2 & 5 & -1 \\
7 & -1 & -2
\end{array}\right]\)

Question 32.

Answer:
(a) \(\frac{-1}{11}, \frac{2}{11}\)

Question 33.
Using elementary transformation, find the inverse of matrix \(\left[\begin{array}{ccc}
-1 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)

Answer:
(a) \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
-8 & 7 & -5 \\
5 & -4 & 3
\end{array}\right]\)

Question 34.
Find the inverse of the matrix \(A=\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\), using elementary row transformation.

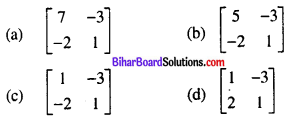
Answer:
(a) \(\left[\begin{array}{cc}
7 & -3 \\
-2 & 1
\end{array}\right]\)

Question 35.

Answer:
(d) \(\frac{1}{2}\)

Question 36.
If A² – A + I = O, then the inverse of A is
(a) I – A
(b) A – I
(c) A
(d) A + I
Answer:
(a) I – A

Question 37.
Total number of possible matrices of order 3 × 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512
Answer:
(d) 512

Question 38.
The matrix \(\left[\begin{array}{ccc}
0 & -5 & 8 \\
5 & 0 & 12 \\
-8 & -12 & 0
\end{array}\right]\) is a
(a) diagonal matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) scalar matrix
Answer:
(c) skew symmetric matrix

Question 39.
If A is a matrix of order m × n and B is a matrix such that AB’ and B’A are both defined, then the order of matrix B is
(a) m × m
(b) n × n
(c) n × m
(d) m × n
Answer:
(d) m × n

Question 40.
If A and B are matrices of the same order, then (AB’ – BA’) is a
(a) skew-symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix
Answer:
(a) skew-symmetric matrix

Question 41.
If A is a square matrix such that A² = I, then (A – I)³ + (A + I)³ – 7A is equal to
(a) A
(b) I – A
(c) I + A
(d) 3A
Answer:
(a) A