Bihar Board 12th Physics Numericals Important Questions Part 2 with Solutions

BSEB Bihar Board 12th Physics Important Questions Numericals Part 2 are the best resource for students which helps in revision.

Bihar Board 12th Physics Numericals Important Questions Part 2 with Solutions

प्रश्न 1.
एक आदमी 1 मीटर से कम दूरी की वस्तु को नहीं देख सकता है: 0.5 मीटर की दूरी पर रखी गयी पुस्तक को पढ़ने के लिए उसे किस प्रकार तथा किस क्षमता के लेन्स का प्रयोग करना होगा।
उत्तर:
प्रश्न से u = – 0.5 m
ν = – 1 m
f = ?
लेन्स के सूत्र से, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
या,
\(\frac{1}{-1}-\frac{1}{-0.5}=\frac{1}{f}\)
या,
-1 + \(\frac{1}{+0.5}=\frac{1}{f}\)
या,
\(\frac{1}{f}=\frac{-0.5+1}{0.5}=\frac{0.5}{0.5}\) = 1
∴ f = 1 मीटर
चूँकि का मान (+ve) है अतः लेन्स, उत्तल (Convex) होगा।
∴ शक्ति = \(\frac{1}{f}=\frac{1}{1}\) = 1D

प्रश्न 2.
एक संयुक्त सूक्ष्मदर्शी के अभिदृश्यक तथा नेत्रिका की फोकस दूरी क्रमशः 4 cm तथा 10 cm है। एक वस्तु अभिदृश्यक से 5 cm की दूरी पर रखा गया है और अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है। सूक्ष्मदर्शी की लम्बाई तथा आवर्द्धक क्षमता निकालें।
उत्तर:
अभिदृश्यक के लिए :
f₀ = 4 cm तथा u₀ = -5cm
लेन्स के सूत्र से,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
या, \(\frac{1}{v_{0}}-\frac{1}{-5}=\frac{1}{4}\)
या, \(\frac{1}{v_{0}}=\frac{1}{4}-\frac{1}{5}=\frac{5-4}{20}=\frac{1}{20}\)
v₀ = 20 cm
नेत्रिक के लिए-
f_e = 10 cm तथा ν_e = -25 cm

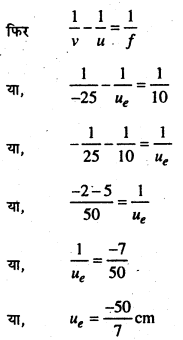
प्रश्न 3.
एक संयुक्त सूक्ष्मदर्शी के अभिदृश्यक की फोकस लम्बाई.3 cm है। अभिदृश्यक से 4 cm की दूरी पर एक वस्तु है। इसको अन्तिम प्रतिबिम्ब नेत्रिका से 30 cm पर बनता है। यदि सूक्ष्मदर्शी की लम्बाई 22 cm हो तो नेत्रिका की फोकस लम्बाई निकालें ।
उत्तर:
अभिदृश्यक के लिए :
f₀ = 3 cm तथा u₀ = -4 cm
सूत्र से,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
या,
\(\frac{1}{v_{0}}-\frac{1}{-4}=\frac{1}{3}\)
या,
\(\frac{1}{v_{0}}+\frac{1}{4}=\frac{1}{3}\)
या,
\(\frac{1}{v_{0}}=\frac{1}{3}-\frac{1}{4}\)
या,
\(\frac{1}{v_{0}}=\frac{4-3}{12}=\frac{1}{12}\)
या = ν₀ 12cm
अतः नेत्रिका से वस्तु की दूरी u_e = सूक्ष्मदर्शी की लम्बाई -V₀
= 22 – 12 = 10 cm.
फिर प्रश्न से, V_e = -30 cm
सूत्र से, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
या, \(\frac{1}{30}-\frac{1}{-10}=\frac{1}{f_{E}}\)
या, \(\frac{1}{30}+\frac{1}{10}=\frac{1}{f_{E}}\) या, \(\frac{-1+3}{30}=\frac{1}{f_{E}}\)
या, \(\frac{2}{30}=\frac{1}{f_{E}}\)
f_E = 15cm.

प्रश्न 4.
एक खगोलीय दूरबीन के अभिदृश्यक तथा नेत्रिका के बीच की दूरी सा, समायोजन के लिए 105 है। इसकी आवर्द्धन क्षमता 20 है। दोनों लेन्सों की फोकस निकालें।
उत्तर:
प्रश्न से, दूरबीन की लम्बाई = 105 cm
m = 20
अब सामान्य समायोजन के लिए,
m = \(\frac{F}{f}\)
या, 20 = \(\frac{F}{f}\)
या, F = 20f
परन्तु दूरबीन की लम्बाई = F + f
105 = 20 f + f
या, 21 f = 105
या, f = 5 cm
फिर F = 20 f
= 20 × 5
= 100 cm

प्रश्न 5.
यंग के प्रयोग में छिद्रों के बीच की दूरी 0.05 cm है। यदि छिद्रों के तर पदों की दूरी 40 cm बढ़ा दी जाय तो धारियों की चौड़ाई 0.04 cm बढ़ जाती है। प्रस्त के तरंग लम्बाई की गणना करें ।
उत्तर:
प्रारम्भ में d = 0.05 cm
∴ λ = \(\frac{0.05 \beta}{D}\) …(1)
जब छिद्रों के तल से पर्दे की दूरी 40 cm बढ़ा दी जाती है तक β का मान (β +0.04) cm हो जाता है।
∴ λ = \(\frac{(\beta+0.04) \times 0 \cdot 05}{D+40}\) …(2)
समी. (1) तथा समी. (2) की तुलना करने पर,
\(\frac{(\beta+0.04) \times 0 \cdot 05}{D+40}=\frac{0 \cdot 05 \beta}{D}\)
या, \(\frac{\beta}{D}=\frac{\beta+0.04}{D+40}\)
या, βD + 40β = βD+ 0.04D
या, 40β = 0.04 D
या, \(\frac{\beta}{D}=\frac{0.04}{40}\)
समी॰ (1) में \(\frac{\beta}{D}\) का मान देने पर,
λ = \(\frac{0.05 \times 0 \cdot 04}{40}\)
= 50 × 10^-5 cm
= 5000 × 10^-8 cm = 5000Å

प्रश्न 6.
यंग के एक प्रयोग में 20 धारियों की चौड़ाई 19.6 mm पाया जाता है । छिद्रों के बीच की दूरी 0.75 mm है । यदि छिद्र से धारी की दूरी 1.25 m हो तो प्रकाश के तरंग लम्बाई का मान निकालें ।
उत्तर:
प्रशन से, β = \(\frac{19 \cdot 6}{20}\) = 0.98 m.
β = 19.6 × 10^-4m
D = 1.25m
d = 0.75mm = 7.5 × 10^-4m
हम जानते हैं कि λ = \(\frac{d \beta}{D}=\frac{7 \cdot 5 \times 10^{-4} \times 9 \cdot 8 \times 10^{-4}}{1 \cdot 25}\)
= 5.88 × 10^-7m

प्रश्न 7.
एक 5 × 10^-8 कूलम्ब आवेश को M बिन्दु से N बिन्दु पर लाया जाता है। समें 8 × 10^-4 जूल कार्य करना पड़ता है। यदि M बिन्दु विभव -2000 volt हो तो N का भव निकलें।
उत्तर:
प्रश्न से, आवेश = 5 × 10^-8 कूलम्ब
कार्य = 8 × 10^-4
जूल M का विभव = -2000 volt
N का विभव (ν) = ?
अब M और N के बीच विभवान्तर = ν – (-2000)
= ν + 2000
∴ किया गया कार्य = आवेश × विभवान्तर .
8 × 10^-4 = 5 × 10^-8 (ν + 2000)
या, ν +2000\(\frac{8 \times 10^{-4}}{5 \times 10^{-8}}=\frac{80000}{5}\) = 160000
या,
ν = 160000 – 2000 = 14000 volt

प्रश्न 8.
पारे की 27 छोटी बूंदों को 3 volt के समान विभव तक आवेशित ति गया है। यदि सभी बूंदों को मिलाकर एक बड़ी बूंद बनाई जाए तो बड़ी बूंद का विभव होगा?
उत्तर:
मानलिया कि एक छोटी बूंद पर आवेश =q
एक छोटी पर त्रिज्या = r
एक छोटी बूंद पर विभव = 3 volt
∴ विभव = \(\frac{1}{4 \pi \in 0} \frac{q}{r}\)
या, 3 = \(\frac{1}{4 \pi \epsilon_{0}} \cdot \frac{q}{r}\) …(1)
मान लिया कि बड़े बूंद की त्रिज्या = R
अब बड़े बूंद का आयतन = 27 छोटे बूंद का आयतन
\(\frac{4}{3}\)πR³ = 27 × \(\frac{4}{3}\)πr³
या,  R³ = 27r³     ∴ R = 3r

= 27 Volt.

प्रश्न 9.
दिये गये चित्र में M और N के बीच समतुल्य धारिता की गणना करें
उत्तर:

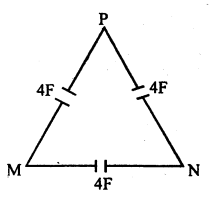
MPN की समतुल्य धारिता, \(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\)
\(=\frac{1}{4}+\frac{1}{4}\)
\(=\frac{2}{4}=\frac{1}{2}\)
या, C = 2F
यह C फिर 4F धारिता से.समानान्तर क्रम में जुड़ा है।
∴ M और N के बीच समतुल्य धरिता = 2 + 4
=6F

प्रश्न 10.
दिये गये चित्र में (a) M और N तथा M और B के बीच समतुल्य धारिता ज्ञात करें।
उत्तर:

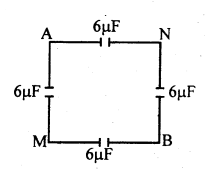
(a) MAN की समतुल्य धारिता,
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\)
\(=\frac{1}{6}+\frac{1}{6}\)
\(=\frac{2}{6}=\frac{1}{3}\)
∴ C = 3μF
फिर MBN में समतुल्य धारिता
\(\frac{1}{C^{\prime}}=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3}\)
∴ C = 3μF
ये दोनों समानान्तर क्रम में रहते हैं
∴ M और N के बीच समतुल्य धारिता = 3 + 3 = 6μF

(b) MANB में समतुल्य धारिता
\(\frac{1}{C}=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\)
\(=\frac{3}{6}=\frac{1}{2}\)
या, C = 2μF
फिर यह C तथा 6F समानान्तर क्रम में जुड़ा है।
∴ M और B के बीच समतुल्य धारिता = 2 + 6
= 8μF.

प्रश्न 11.
दिये गये चित्र में (a) M और B (b) M और N के बीच समतुल्य धारिता निकालें।
उत्तर:

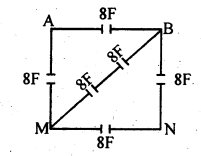
(a) MAB में समतुल्य धारिता,
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\)
\(=\frac{1}{8}+\frac{1}{8}=\frac{2}{8}=\frac{1}{4}\)
या, C = 4F
फिर MNB के बीच समतुल्य धारिता,
C’ = 4F
इसी प्रकार M और B के बीच समतुल्य धारिता
= 4F
ये तीनों फिर समानान्तर क्रम में जुड़े हैं।
∴ M और B के बीच समतुल्य धारिता
= 4 + 4 + 4 = 12 F

(b) MAB की समतुल्य धारिता = 4F
फिर MB ” ” ” = 4F
ये तीनों समानान्तर क्रम में है।
∴ समतुल्य धारिता = 4 + 4 = 8F
जो BN (8F) के साथ श्रेणी क्रम में है।
∴ समतुल्य धारिता = 4F
जो फिर MN (8F) के साथ समानान्तर क्रम में है।
∴ M और N के बीच समतुल्य धारिता = 4 + 8
= 12 F

प्रश्न 12.
दिये गये चित्र में A और C के बीच समतुल्य धारिता का मान निकालें।
उत्तर:

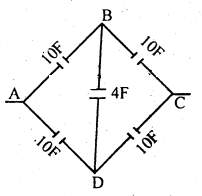
दिया गया चित्र Wheat stone bridge के सिद्धान्त पर काम करता है। इससे B और D का विभव समान हो जाता है। अत: 4F का कोई प्रभाव नहीं पड़ता है।
∴ ABC के बीच समतुल्य धारिता
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\)
\(=\frac{1}{10}+\frac{1}{10}=\frac{2}{10}=\frac{1}{5}\)
∴ C = 5 F
इसी प्रकार ABC के बीच समतुल्य धारिता
C’ = 5 F
फिर ये दोनों C तथा C’ समानान्तर क्रम में है
∴ A और C के बीच समतुल्य धारिता
= 5 + 5 = 10F

प्रश्न 13.
दिये गये चित्र से संधारित्रों की धारिता 20F, 30F तथा 15F है। A पर विभव 99V है। दूसरे अर्थात् C₂ के बीच विभवान्तर ज्ञात करें।
उत्तर:

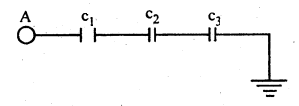
चित्र के आधार पर C₁, C₂ तथा C₃ श्रेणीक्रम में जुड़े हैं।
∴ \(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\)
\(=\frac{1}{20}+\frac{1}{30}+\frac{1}{15}\)
\(=\frac{3+2+4}{60}\)
\(=\frac{9}{60}=\frac{3}{20}\)
∴ C = \(\frac{20}{3}\)F
अत: आवेश (Q) = CV
= \(\frac{20}{3}\) .90
= 600 कूलम्ब

प्रश्न 14.
एक बिन्दु आवेश से 10 cm की दूरी पर एक बिन्दु पर विद्युत क्षेत्र की तीव्रता निकालें । उस बिन्दु पर विभव.3000 volt.
उत्तर:
यहाँ ν = 3000 वोल्ट
r = 10 cm = 0.1 m

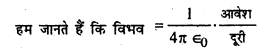
3000 = 9 × 10⁹\(\frac{Q}{0 \cdot 1}\)
या, Q = \(\frac{3000 \times 0 \cdot 1}{9 \times 10^{9}}=\frac{1}{3}\) × 10^-7C

= 9 × 10⁹ × \(\frac{1}{3}\) × 10⁷ \(\frac{1}{(0 \cdot 1)^{2}}\)
= 3 × 10² × 10²
= 3000 ν/m